数据结构入门
数据结构(data structure)
什么是数据结构?
数据结构是计算机中存储、组织数据的方式。
数据结构是一种具有一定逻辑关系,在计算机中应用某种存储结构,并且封装了相应操作的数据元素集合。它包含三方面的内容,逻辑关系、存储关系及操作。
不同种类的数据结构适合于不同种类的应用,而部分甚至专门用于特定的作业任务。例如,计算机网络依赖于路由表运作,B 树高度适用于数据库的封装。常见的数据结构
栈(Stack):栈是一种特殊的线性表,它只能在一个表的一个固定端进行数据结点的插入和删除操作。
队列(Queue):队列和栈类似,也是一种特殊的线性表。和栈不同的是,队列只允许在表的一端进行插入操作,而在另一端进行删除操作。
数组(Array):数组是一种聚合数据类型,它是将具有相同类型的若干变量有序地组织在一起的集合。
链表(Linked List):链表是一种数据元素按照链式存储结构进行存储的数据结构,这种存储结构具有在物理上存在非连续的特点。
树(Tree):树是典型的非线性结构,它是包括,2 个结点的有穷集合 K。
图(Graph):图是另一种非线性数据结构。在图结构中,数据结点一般称为顶点,而边是顶点的有序偶对。
数组
快速排序
QuickSort 是一种基于 “分而治之 “算法的排序算法,它选取一个元素作为枢轴,并通过将枢轴置于排序数组中的正确位置,围绕选取的枢轴对给定数组进行分区。
过程图示
逻辑很简单,我们从最左侧的元素开始,并以 i 为单位跟踪较小(或相等)元素的索引。在遍历过程中,如果发现较小的元素,我们就将当前元素与 arr[i] 互换。否则,我们将忽略当前元素。
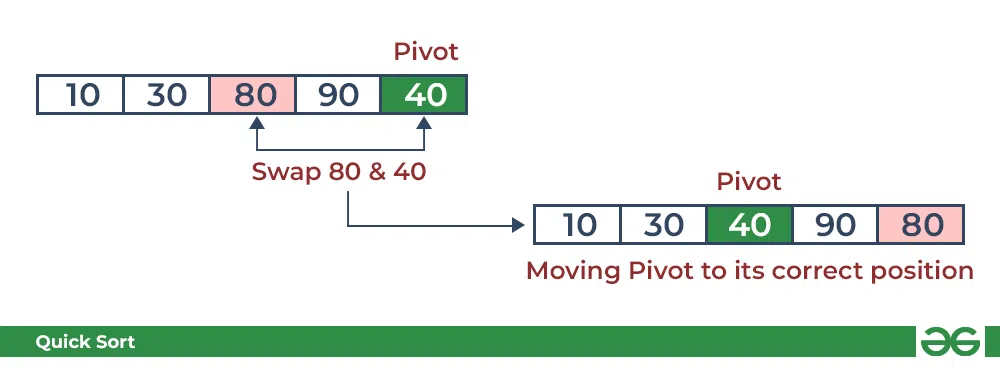
1.考虑:arr[] = {10、80、30、90、40}
- 将 10 与中位数进行比较,如果小于中位数,则逐级排列。
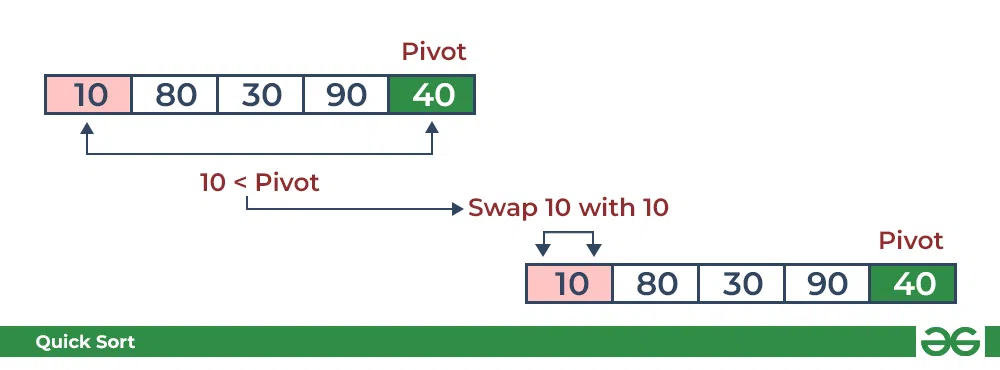
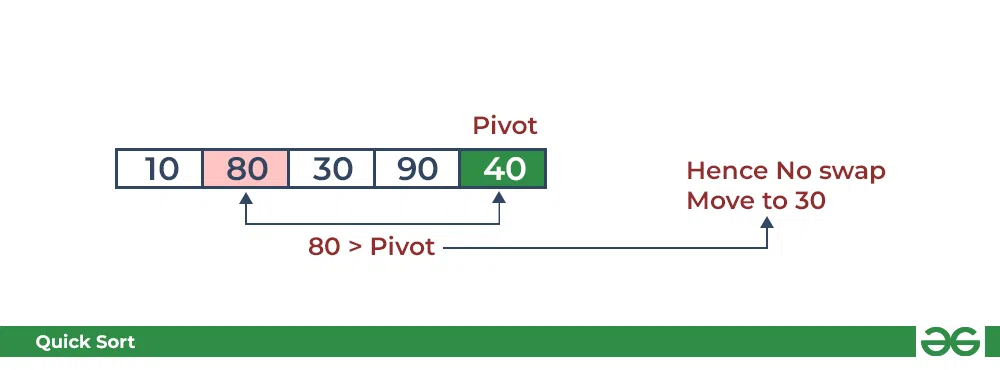
- 将 80 与pivot进行比较。它大于枢轴。
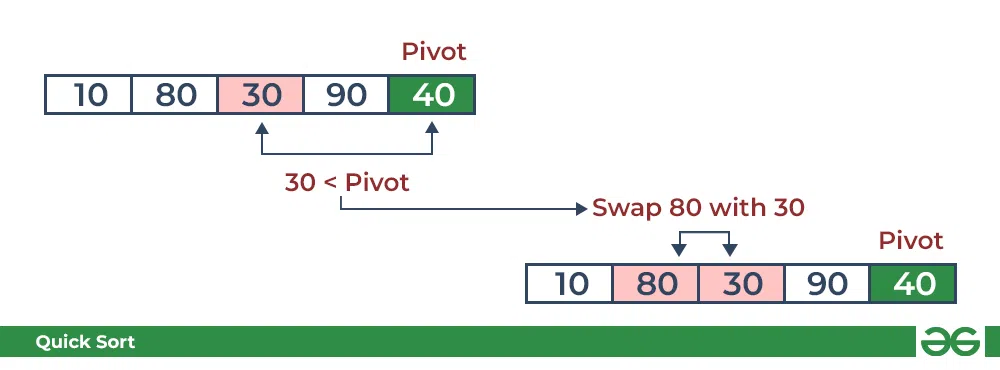
- 比较 30 和pivot。它小于pivot,因此相应地进行排列。
- 比较90和pivot,它大于pivot
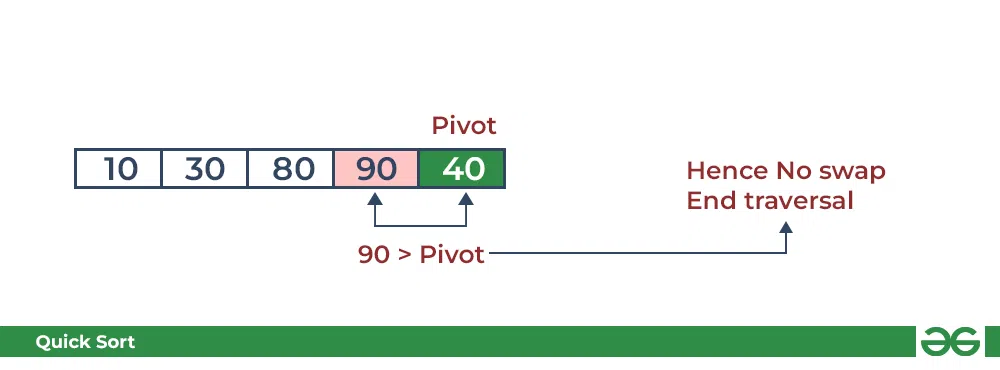
- 将目标放在正确的地方
具体实现的代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
int partition(int arr[],int low,int high)
{
//选择pivot
int pivot=arr[high];
//较小元素的索引并表示
//到目前为止找到的pivot的正确位置
int i=(low-1);
for(int j=low;j<=high;j++)
{
////如果当前元素小于 pivot
if(arr[j]<pivot)
{
i++;
swap(arr[i],arr[j]);
}
}
swap(arr[i+1],arr[high]);
return (i+1);
}
void quickSort(int arr[],int low,int high)
{
if(low<high)
{
// pi是pivot的分区返回索引
int pi=partition(arr,low,high);
/*
比枢轴小的放在左边;
比枢轴大的放在右边;
*/
quickSort(arr,low,pi-1);
quickSort(arr,pi+1,high);
}
}
int main() {
int arr[]={10,7,8,9,1,5};
int n=sizeof(arr)/sizeof(arr[0]);
// 调用函数
quickSort(arr,0,n-1);
//打印快排数组
printf("Sorted Array\n");
for(int i=0;i<n;i++)
{
printf("%d",arr[i]);
printf(" ");
}
return 0;
}
链表
在学习链表前我们需要知道什么是动态内存;
动态内存
1 | void mallocFn() { |
注意
使用了malloc去开辟了你的内存后,一定在你代码结束的时候,或者你不需要使用这一块内存时,一定要及时的free笔者在写这一段时发现了一篇不错的博客,非常细致的讲解了malloc的原理深入理解malloc
现在我们回到链表
链表是线性结构,在内存中非连续存储数据元素的一种数据结构,它是离散分布的。每个节点通过指针相连,每个一个前驱节点点和后续节点,头节点无前驱节点,尾节点无后续节点。
链表的种类:单链表、双链表、循环链表
双链表、循环链表是在单链表基础上扩展,下面是单链表结构:1
2
3 头结点:A 首节点:B 尾节点:C
👇 👇 👇
[data=NULL|next]——>[data|next]——>[data|next]——>[data|next]——>[data|next]——> NULL
头结点: 第一个有效节点之前的节点,不存放有效数据,加头结点的目的主要是为了方便链表操作;
首节点:第一个有效节点;
尾节点:最后一个有效节点;
头指针:指向头结点的指针变量;
尾指针:指向尾结点的指针变量;
确定一个链表只需要一个参数:头指针;链表中单个节点的数据类型:
1 | struct Node { |
示例如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65//用C语言写一个链表
typedef struct node
{
int data; //数据域
struct node *next; //指针域
} Node;
Node *createList(int n) //创建链表
{
Node *head = NULL;
Node *p = NULL;
Node *temp = NULL;
int i = 0;
for (i = 0; i < n; i++) //循环创建链表
{
temp = (Node *)malloc(sizeof(Node));
printf("请输入第%d个节点的值:", i + 1);
scanf("%d", &(temp->data));
temp->next = NULL;
if (head == NULL)
{
head = temp;
}
else
{
p = head;
while (p->next != NULL)
{
p = p->next;
}
p->next = temp;
}
}
return head;
}
//打印链表
void printList(Node *head)
{
Node *p = head;
while (p != NULL)
{
printf("%d ", p->data);
p = p->next;
}
}
int main()
{
int n = 0;
Node *head = NULL;
printf("请输入链表的长度:");
scanf("%d", &n);
head = createList(n);
printList(head);
return 0;
}
栈(stack)
堆栈是一种遵循先进后出(FILO)协议的数据结构。最新添加到堆栈中的节点就是有资格首先被移除的节点。如果有三个节点(a、b 和 c)以完全相同的顺序添加到堆栈中,则必须先删除节点 c。移除或返回节点 a 值的唯一方法就是移除节点 c 和 b。

栈分为静态栈和动态栈,静态栈通常由数组构成,动态栈通常由链表构成(都只有一个出入口);以动态栈为🌰,确认一个栈的节点,只需要两个参数,顶部节点和尾部节点。
1 | struct Stack { |
你可以把栈想象成一个停着很多辆车的车库🚃,你只有将外面停着的车🏎开走,才能让里面的车开出来
堆栈数据结构有三个主要方法:push()、pop() 和 peek()。
- push() 方法将一个节点添加到栈顶。
- pop()方法从栈顶删除一个节点。
- peek() 方法返回栈顶节点的值,但不会将其从栈中移除。
队列(queue)
- 队列遵循先进先出协议。队列是一种由节点组成的数据结构,遵循先进先出(FIFO)协议。
这就好比阳光长跑排队,队列中的第一位同学先刷脸。
队列分为链式队列和静态队列,前者使用链表实现,后者是数组实现(都是一头出,一头入);
下面是以静态队列为例子讲解。对于静态队列,它由数组构成,存储空间是一定的,而为了避免出现空间浪费的问题,它就必须是一个循环队列(静态队列必须是循环队列);一个循环队列只需要两个参数:front(头)、rear(尾);
不同场合front和rear不同的含义:
队列初始化:front 和 rear 值都是0;
队列非空:front代表队列的第一个元素;rear代表得失队列最后一个有效元素的下一个元素;
队列为空:front和rear值相等,但不一定是0;
队列算法核心:
入队算法:rear = (rear+1)%数组长度;
出队算法:front = (front+1)%数组长度;
队列数据结构有三种主要方法:
- enqueue(将节点添加到队列后部)
- dequeue(删除队列前面的节点)
- peek(返回队列前部节点的值,但不删除该节点)
代码示例:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116//用C语言写一个队列,实现队列的基本操作
//定义队列结构体
typedef struct Queue
{
int data[MAXSIZE];
int front;
int rear;
} Queue;
//初始化队列
void initQueue(Queue *q)
{
q->front = 0;
q->rear = 0;
}
//判断队列是否为空
int isEmpty(Queue *q)
{
if (q->front == q->rear)
{
return 1;
}
else
{
return 0;
}
}
//判断队列是否已满
int isFull(Queue *q)
{
if ((q->rear + 1) % MAXSIZE == q->front)
{
return 1;
}
else
{
return 0;
}
}
//入队
int enQueue(Queue *q, int data)
{
if (isFull(q))
{
printf("队列已满,无法入队\n");
return 0;
}
else
{
q->data[q->rear] = data;
q->rear = (q->rear + 1) % MAXSIZE;
return 1;
}
}
//出队
int deQueue(Queue *q, int *data)
{
if (isEmpty(q))
{
printf("队列为空,无法出队\n");
return 0;
}
else
{
*data = q->data[q->front];
q->front = (q->front + 1) % MAXSIZE;
return 1;
}
}
//打印队列
void printQueue(Queue *q)
{
if (isEmpty(q))
{
printf("队列为空\n");
}
else
{
int i = q->front;
while (i != q->rear)
{
printf("%d ", q->data[i]);
i = (i + 1) % MAXSIZE;
}
printf("\n");
}
}
int main()
{
Queue q;
initQueue(&q);
enQueue(&q, 1);
enQueue(&q, 2);
enQueue(&q, 3);
printQueue(&q);
int data;
deQueue(&q, &data);
printf("出队元素:%d\n", data);
printQueue(&q);
return 0;
}
树(Tree)
树是由有向(或无向)边连接的节点集合。与数组、链表、堆栈和队列等线性数据结构相比,树是一种非线性数据结构。树可以是空的,没有节点,也可以是由一个称为根的节点和零个或一个或多个子树组成的结构。
树具有以下一般特性:
- 一个节点被区分为根节点;
- 每个节点(根节点除外)都有一条有向边与另一个节点相连;
- 一条有向边的走向是:父节点 -> 子节点
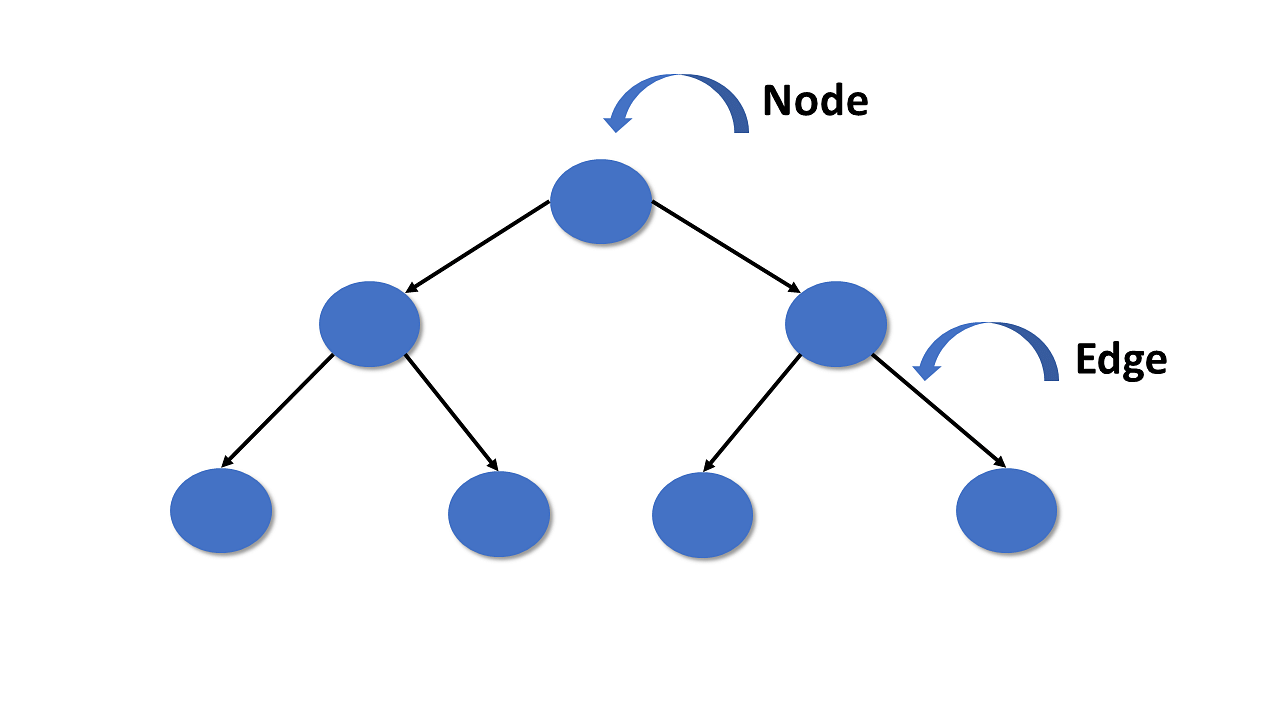
这里我们以二叉树为例进行详细的解释:
二叉搜索树
在二叉搜索树中,父节点最多可以有两个子节点。这些子节点被称为 “左子节点 “和 “右子节点”。二叉搜索树要求左子节点存储的值小于父节点的值,而右子节点存储的值大于父节点的值。
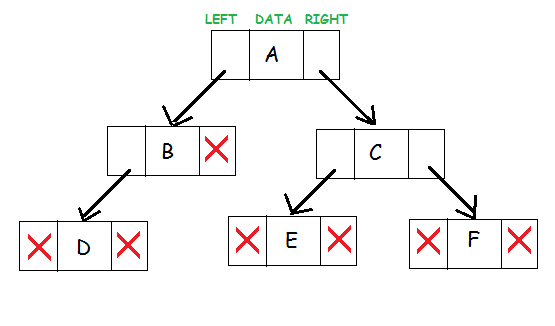
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184//用C语言实现二叉树的创建、遍历、查找、插入、删除等操作
typedef struct BiTNode
{
int data;
struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;
//创建二叉树
void CreateBiTree(BiTree *T)
{
int ch;
scanf("%d", &ch);
if (ch == -1)
*T = NULL;
else
{
*T = (BiTree)malloc(sizeof(BiTNode));
if (!*T)
exit(-1);
(*T)->data = ch;
CreateBiTree(&(*T)->lchild);
CreateBiTree(&(*T)->rchild);
}
}
//先序遍历二叉树
void PreOrderTraverse(BiTree T)
{
if (T == NULL)
return;
printf("%d ", T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
//中序遍历二叉树
void InOrderTraverse(BiTree T)
{
if (T == NULL)
return;
InOrderTraverse(T->lchild);
printf("%d ", T->data);
InOrderTraverse(T->rchild);
}
//后序遍历二叉树
void PostOrderTraverse(BiTree T)
{
if (T == NULL)
return;
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
printf("%d ", T->data);
}
//查找二叉树中是否存在某个值
BiTree SearchBST(BiTree T, int key)
{
if (!T || T->data == key)
return T;
if (key < T->data)
return SearchBST(T->lchild, key);
else
return SearchBST(T->rchild, key);
}
//插入二叉树节点
int InsertBST(BiTree *T, int key)
{
if (!*T)
{
*T = (BiTree)malloc(sizeof(BiTNode));
(*T)->data = key;
(*T)->lchild = (*T)->rchild = NULL;
return 1;
}
else if (key == (*T)->data)
return 0;
else if (key < (*T)->data)
return InsertBST(&(*T)->lchild, key);
else
return InsertBST(&(*T)->rchild, key);
}
//删除二叉树节点
int Delete(BiTree *p)
{
BiTree q, s;
if ((*p)->rchild == NULL)
{
q = *p;
*p = (*p)->lchild;
free(q);
}
else if ((*p)->lchild == NULL)
{
q = *p;
*p = (*p)->rchild;
free(q);
}
else
{
q = *p;
s = (*p)->lchild;
while (s->rchild)
{
q = s;
s = s->rchild;
}
(*p)->data = s->data;
if (q != *p)
q->rchild = s->lchild;
else
q->lchild = s->lchild;
free(s);
}
return 1;
}
int DeleteBST(BiTree *T, int key)
{
if (!*T)
return 0;
else
{
if (key == (*T)->data)
return Delete(T);
else if (key < (*T)->data)
return DeleteBST(&(*T)->lchild, key);
else
return DeleteBST(&(*T)->rchild, key);
}
}
int main()
{
BiTree T = NULL;
int key;
printf("请输入二叉树的结点,-1表示空结点:\n");
CreateBiTree(&T);
printf("先序遍历二叉树:\n");
PreOrderTraverse(T);
printf("\n中序遍历二叉树:\n");
InOrderTraverse(T);
printf("\n后序遍历二叉树:\n");
PostOrderTraverse(T);
printf("\n请输入要查找的值:\n");
scanf("%d", &key);
if (SearchBST(T, key))
printf("查找成功!\n");
else
printf("查找失败!\n");
printf("请输入要插入的值:\n");
scanf("%d", &key);
if (InsertBST(&T, key))
printf("插入成功!\n");
else
printf("插入失败!\n");
printf("请输入要删除的值:\n");
scanf("%d", &key);
if (DeleteBST(&T, key))
printf("删除成功!\n");
else
printf("删除失败!\n");
printf("先序遍历二叉树:\n");
PreOrderTraverse(T);
printf("\n中序遍历二叉树:\n");
InOrderTraverse(T);
printf("\n后序遍历二叉树:\n");
PostOrderTraverse(T);
return 0;
}
图(graphs)
数据结构中的图是由有限数量的节点或顶点以及连接它们的边组成的非线性数据结构。
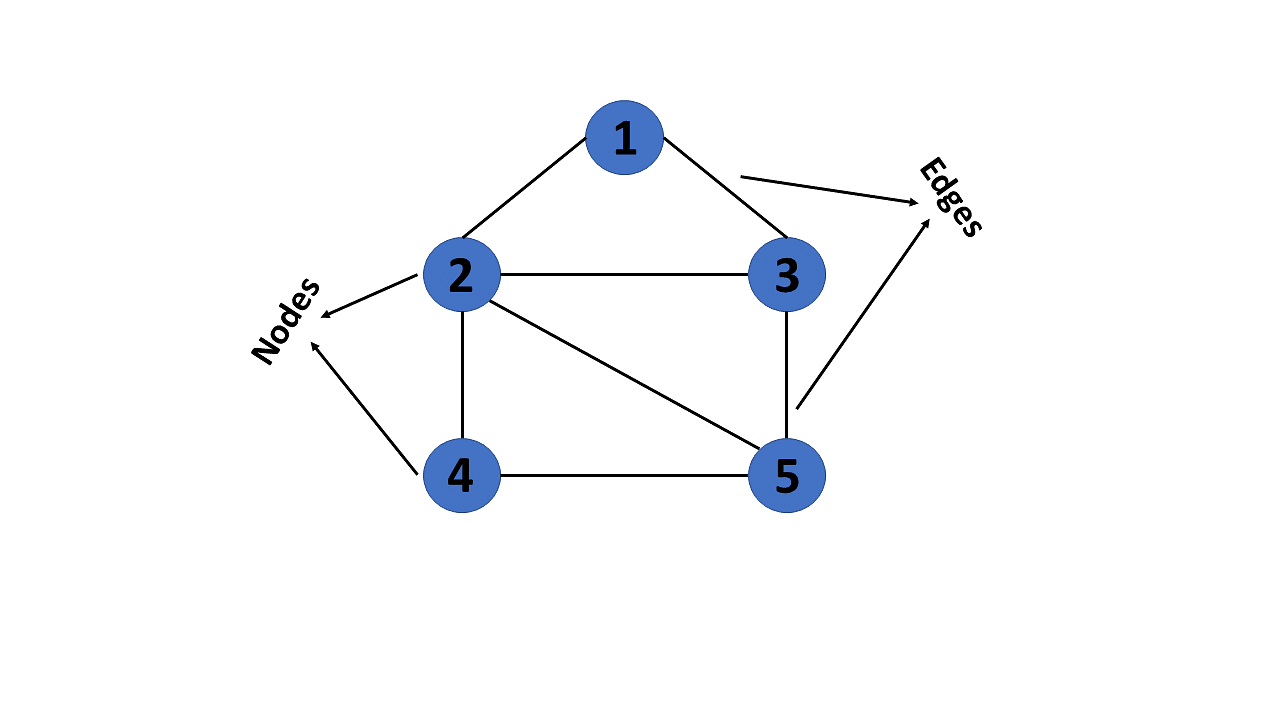
图这里可以深挖的东西有太多,有专门的书叫图论来研究这方面的知识,我们只是简单的讲解一下,笔者在这里也借鉴了一下其他人的文章理解数据结构中的图知识
图表类型:
- 有向图(有向图):边有方向。
- 无向图:边没有方向。
- 加权图:每条边都有一个权重或成本。
- 未加权图:边没有权重。
- 循环图:包含循环(循环)。
- 非循环图:没有循环。
遍历算法:
- 深度优先搜索(DFS):在回溯之前尽可能远地探索。
- 广度优先搜索(BFS):逐层探索。
应用:
- 图对各种现实场景中的关系、网络和依赖关系进行建模。
- 例子包括社交网络、交通系统和互联网。
代码示例:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47//C语言实现简单的数据结构中的图
typedef char VertexType;
typedef int EdgeType;
typedef struct
{
VertexType vexs[MAXVEX]; //顶点表
EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵,可看作边表
int numVertexes, numEdges; //图中当前的顶点数和边数
}MGraph;
//建立无向网图的邻接矩阵表示
void CreateMGraph(MGraph *G)
{
int i, j, k, w;
printf("输入顶点数和边数:\n");
scanf("%d,%d", &G->numVertexes, &G->numEdges); //输入顶点数和边数
for(i = 0; i < G->numVertexes; i++) //读入顶点信息,建立顶点表
scanf(&G->vexs[i]);
for(i = 0; i < G->numVertexes; i++) //矩阵初始化
for(j = 0; j < G->numVertexes; j++)
G->arc[i][j] = INFINITY;
for(k = 0; k < G->numEdges; k++) //读入numEdges条边,建立邻接矩阵
{
printf("输入边(vi,vj)上的下标i,下标j和权w:\n");
scanf("%d,%d,%d", &i, &j, &w); //输入边(vi,vj)上的权w
G->arc[i][j] = w;
G->arc[j][i] = G->arc[i][j]; //因为是无向图,矩阵对称
}
}
int main()
{
MGraph G;
CreateMGraph(&G);
return 0;
}
总结
这篇文章只是简单梳理了几种数据结构类型,每种类型都有更深刻和广泛的用法,但我们不搞ACM,算法只是我们使用的工具而以,不需要死磕某种算法,也不要因为没有做出或者学不明白而懊恼,你只需要了解会使用,或者当你需要的时候能想到这个东西是做什么的就足够了,工程师不必止步于数据结构和算法,你的未来还很远! 💐💐💐






